I was also already asked by someone if this is to replace the MG, since it essentially does the same (keep the crosshair on enemy as long as possible and spray). No idea on that one, but I feel that'd be a step backward at this time, since the MG actually has a good wepon model, has been balanced, and code which works.
Anyway, I dedicated Friday to add some effects to the gun, as I so shortsightedly volunteered to Mario.
Now I don't know at all what this weapon was envisioned to be, so I tried to add some LG-like particle effects, though the result fell short of what I was trying for.
While doing that, I found the code still somewhat flawed, and I'm not sure we can fix it without divVerent's help.
The intended effect is great (a beam trail that behaves realistically, like a water hose) by using stiched-together vertexes instead of (just) particle effects,
and it has, afaik, the most complex weapon code in the game so far as a result.
But the beam drawing is done all client-side, as is the hit indication, making it pretty much a guessing game that doesn't at all indicate a verified hit by the server, as divVerent already pointed out in the code.
You can see how that fails when you pause the game or use slowmo -- the beam will still behave as if in realtime.
Without particle effects it's not as obvious, but once I added some to the trail it is, since they keep getting spawned while the game is paused; which looks truly atrocious.
In reality the beam should freeze while paused, or slow down in slowmo, as does every other wepons shot. I can't say how much work it would be to fix that.
Some screenshots to close with:
The beam as of now:
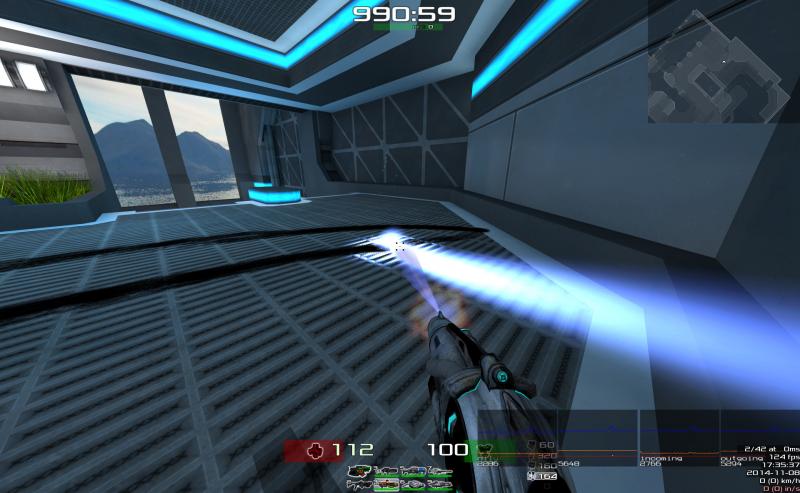

Added particle effects, sadly looks more like electro discharge than fizzling lightning :|
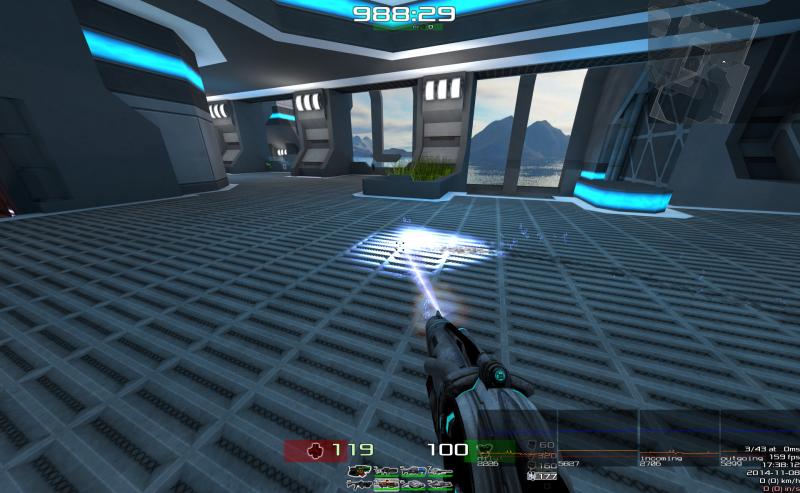

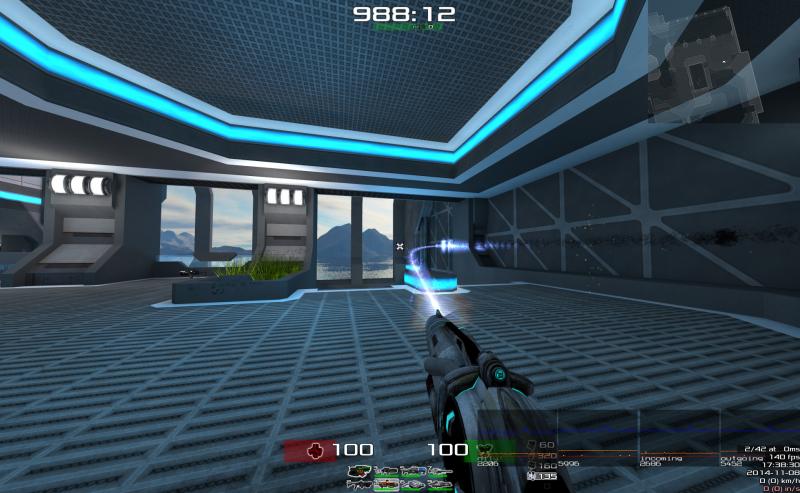
I haven't figured out yet where that muzzleflash comes from, or I'd have removed/changed it

And where it fails...
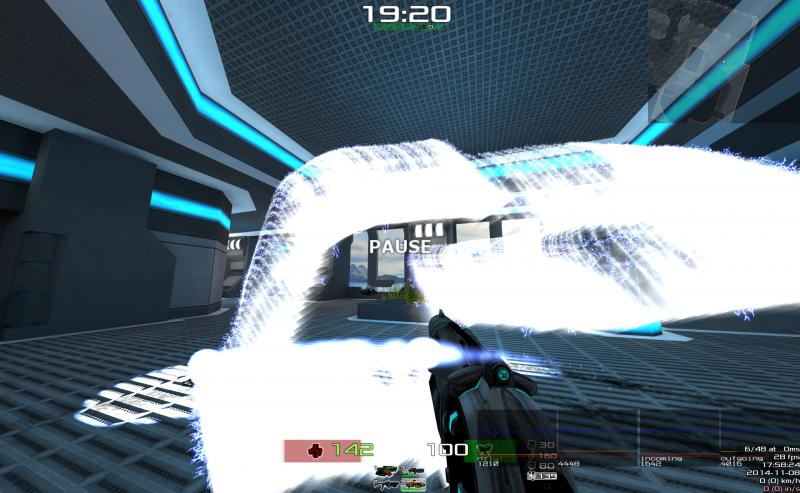
![[Image: 230.png]](http://stats.xonotic.org/static/badges/230.png)



 )
)

![[Image: 22172.png]](http://stats.xonotic.org/static/badges/archer/22172.png)
